Hi, this is Anthony.
I’ve not written a blog post about the vision stuff yet because I’ve been too busy actually working on it. The competition is done now though, and so I have free time to talk about what I’ve learned.
Basically, there are two parts to the generic object detection problem: detection and classification.
Detection is the process of actually locating parts of some image that might be an object. These are referred to as regions of interest. The following image is my rectangle contour detector in action:

There are many ways that detection can be solved. At first I attempted using a Faster R-CNN; a kind of neural network that is trained to find areas of an image that might be an object. Google has a pretrained model called ‘inception’ that I planned on using. However, this was both overkill and too difficult to do in the time.
I also tried doing simple contour detection using binary thresholding, which was far too unreliable.
In the end, I settled with canny edge detection, a more robust method of detecting edges, combined with use of an image pyramid and a sliding window to make sure that all contours were seen.
An image pyramid is simply a series of the same image except scaled down each time. The following image pyramid has a scale factor of 2, where the dimensions of each image are 1/2^n times the dimensions of the base image, where n is the level they are at (0 being the base level).
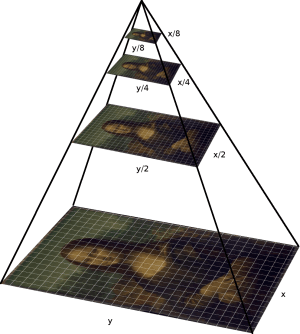
(pyimagesearch, 2015)
The following python function generates an image pyramid:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | def pyramid(image, scale=1.5, minSize=(30, 30)): ODim = image.shape[1] # yield the original image yield (image, 1) # keep looping over the pyramid while True: # compute the new dimensions of the image and resize it w = int(image.shape[1] / scale) image = imutils.resize(image, width=w) ratio = ODim/float(image.shape[1]) # if the resized image does not meet the supplied minimum # size, then stop constructing the pyramid if image.shape[0] < minSize[1] or image.shape[1] < minSize[0]: break # yield the next image in the pyramid yield (image, ratio) |
Larger contours are more difficult to detect than smaller contours, because they are less consistent. There may be small breaks in the contour etc. that the computer can not pick up. By shrinking the image, we can pick up larger contours more accurately.
A sliding window moves across an image and inspects a small part each time, as shown below, like inspecting something with a torch. This helps us to find more contours.
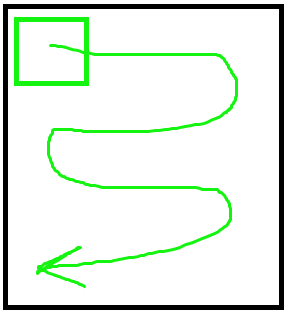
The sliding window is run over each level of the pyramid. This means that if a contour is too big to fit inside the sliding window on a lower level, it will be seen in an upper level where it has been scaled down (but the sliding window remains the same size).
The following python function generates a “sliding window” (array of windows that can be iterated over):
1 2 3 4 5 6 7 | # generates a sliding window (really just a list of image regions. 'sliding' is just a visualization) def sliding_window(image, stepSize, windowSize = (128, 128)): # slide a window across the image for y in range(0, image.shape[0], stepSize): for x in range(0, image.shape[1], stepSize): # yield the current window yield (x, y, image[y:y + windowSize[1], x:x + windowSize[0]]) |
When a contour is found inside the sliding window, two operations are performed on it: translation and dilation.
If we find a contour on the base of the pyramid, the dilation does not need to occur – only the translation. So, I will explain the translation part in an example with the base level of the pyramid.

Each point in the contour has an x and a y coordinate relative to the sliding window, and the sliding window has an x and y coordinate relative to the main image. When we add them together, it allows us to place the contour in the main image. This is the translation part done.
However, if we are on a higher level of the pyramid, more calculations need to occur after this translation so that the contour can be drawn on the original image (base level of the pyramid).
Let’s assume the scale factor is 2: so the level of the pyramid we are on is half (1/2) the length and half the height of the base. I will expand my explanation to fit some scale factor n afterwards.
If the scale factor is 2, you can imagine that each pixel has had its x and y value halved: so a pixel that was at (10, 14) on the original image is now at (5, 7) on the current level of the pyramid. If we have a contour at (5, 7) on the current level of the pyramid, then we know there will be a contour close to (10, 14) on the base level.
For the scale factor n, we replace ‘half’ with ‘1/n’ and ‘double’ with ‘n’. If the base has width and height of n times the width and height of our current level, then all the contours we find at the current level have to be multiplied by n.
Combining this translation and dilation, we can come up with a formula. Let (x1,y1) be the coordinates of the contour relative to the sliding window. Let (x2,y2) be the coordinates of the sliding window relative to the current level of the pyramid. Let n be the scale factor between the current level of the pyramid and the base level. We can deduce that:
x (on base) = n(x1+x2)
y (on base) = n(y1+y2)
This formula is implemented in the program. All the contours are now ready to be applied to the original image on the base of the pyramid. The following python code uses the pyramid function and sliding window function defined earlier to find contours, and translates and dilates them so they can be placed on the original image.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | # utilizing the functions base_level_of_pyramid = cv2.imread("path/to/your/image") for current_level_of_pyramid, current_ratio in pyramid(base_level_of_pyramid, scale=2): for sliding_window_x, sliding_window_y, window in sliding_window(current_level_of_pyramid, 32): # use your method of finding contours here. make sure they are an array of points # in the form [[x, y], [x, y], [x, y]....] for the following code to work. beware that # most contour detection functions in opencv store the points in two layers of # array, like [[[x,y]], [[x,y]], [[x,y]], [[x,y]].....] contours = ..... new_contours = [] for point in contours: # compute the coordinates on the base by translation and dilation x_on_base = current_ratio * (point[0] + sliding_window_x) y_on_base = current_ratio * (point[1] + sliding_window_y) # add them to the 'new contours' which will be drawn new_contours.append([x_on_base, y_on_base]) |
For further reading, I recommend Adrian Rosebrock’s blog pyimagesearch.
